Test mathématique: Fonction
Rappel de base
Définition - Fonction
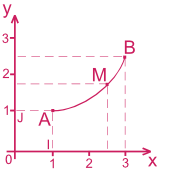
Repère cartésien orthonormé :
- Droites (Ox) et (Oy) sont perpendiculaires
-OI = OJ = 1Coordonnées du point
M (xM, yM):xMest l'abscisse de MyMest l'ordonnée de M
Rappel de base
Définition - Fonction
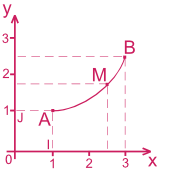
Repère cartésien orthonormé :
- Droites (Ox) et (Oy) sont perpendiculaires
-OI = OJ = 1Coordonnées du point
M (xM, yM):xMest l'abscisse de MyMest l'ordonnée de MPour chaque valeur de
x, abscisse d'un point M de la courbe, on peut faire correspondre la valeury, ordonné de ce pointExemple : Coordonnées du point
A (1, 1)et du pointB (3, 2.5)
Ainsi
yest fonction dex:y = f(x).
xest une variable et a pour imageypar la fonctionf.La représentation de cette fonction correspond à l'ensemble des points qui ont pour coordonnées
(x ; y = f(x)).
f(x) = ax + best une fonction affineSi
b = 0,f(x) = axest une fonction linéaireSi
a = 0;f(x) = best une fonction constante
aest un nombre réel appelé coefficient directeur ou coefficient de proportionnalité
best l'ordonnée à l'origine
Fonction linéaire

Dans un repère du plan,
y = f(x) = axest l'équation d'une droite passant par l'origine du repère(0,0); c'est une fonction linéaire.Dans cet exemple, la fonction linéaire est de la forme
f(x) = axdoncf(3) = 3a = 2d'oùa = 2⁄3etf(x) = 2⁄3 xouy = 2⁄3 x.On peut déterminer un autre point de cette droite en calculant les coordonnées d'un de ses points : si
x = 2, alorsy = 2⁄3 x 2 = 4⁄3.
Fonction affine
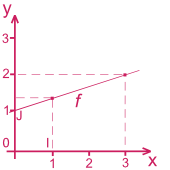
Dans un repère du plan,
y = f(x) = ax + best l'équation d'une droite; c'est une fonction affine.Dans cet exemple, la fonction linéaire est de la forme
f(x) = ax + bdoncf(0) = 0a + b = 1d'oùb = 1etf(3) = 3a + b = 3a + 1 = 2d'oùa = 1⁄3. Ainsif(x) = 1⁄3 x + 1ouy = 1⁄3 x + 1.On peut déterminer un autre point de cette droite en calculant les coordonnées d'un de ses points : si
x = 1, alorsy = 1⁄3 x 1 + 1 = 4⁄3.Pour calculer le coefficient d'une fonction affine f à partir de deux points, il suffit d'appliquer la formule suivante :
a = yA - yB⁄xA - xBPar exemple :
A (0;1)etB (3;2)alorsa = 1 - 2⁄0 - 3 = 1⁄3
Droite parallèle à l'axe des abscisses
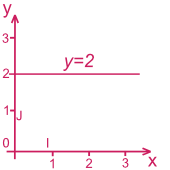
y = aest l'équation d'une droite parallèle à l'axe des abscissesExemple :
y = 2
Droite parallèle à l'axe des ordonnées
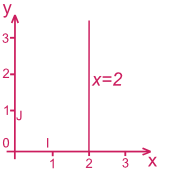
x = aest l'équation d'une droite parallèle à l'axe des ordonnéesExemple :
x = 2
Droites parallèles
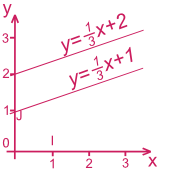
y = ax + bety = a'x + bsont deux équations de droites; sia = a'les droites sont parallèles.Exemple :
a = a' = 1⁄3
Droites perpendiculaires
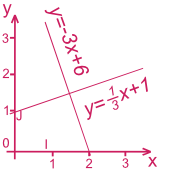
y = ax + bety = a'x + bsont deux équations de droites; sia x a' = -1les droites sont perpendiculaires.Exemple :
a x a' = -1⁄3 x 3 = -1
Résolution graphique des équations du premier degré à deux inconnus
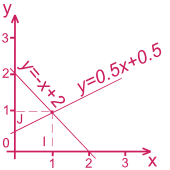
Un système de deux équations à deux inconnues se présente sous la forme :
ax + by = ceta'x + b'y = c'oùa,b,c,a',b',c'sont connus.Résoudre un système de deux équations à deux inconnues, c'est trouver les couples
(x;y)qui sont solutions des deux équations.Exemple :
x + y = 2et0.5x - y = - 0.5
Sous la forme d'une équation de droite :y = -x +2ety = 0.5x + 0.5
Une fois les droites tracées, les coordonnées du point d'intersection des deux droites est la solution du système, soit(1;1).
On peut vérifier la solution en remplaçant le couple(x;y)par(1;1)dans les deux équations :x + y = 1 + 1 = 2et0.5 - 1 = - 0.5
Accueil > Test psychotechnique > Test mathématique > Test mathématique: Fonction