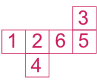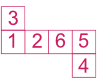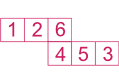Cube

Le test des cubes est un exercice de représentation dans l'espace. Il teste les capacités spatiales d'un individu à identifier, par exemple, la face opposée d'un cube, le cube obtenu à partir d'un cube à plat, ou encore le nombre de cubes d'une structure.

Géométrie du cube

Les principales priorités d'un cube à connaître pour réussir les tests de cube sont listées ci-dessous.

Un cube à 6 faces

Seulement 3 faces sont visibles en même temps

Règle 1 : Deux faces opposées ne peuvent pas être adjacentes les unes aux autres

Les faces visibles ne peuvent jamais être en opposition l'une de l'autre.

Exemple :
Quelle lettre est à l'opposé de la lettre A?
Réponse : la lettre C. En sachant que les 3 faces visibles ne peuvent pas être opposées, les figures 1 et 2 nous permettent d'éliminer les lettres B, D et E. La figure 3 nous confirme que la lettre opposée à A est C.

Règle 2 : Si pour 2 dés, 2 faces sont adjacentes et l'une des 2 faces est à la même position, alors les 2 autres faces visibles sont opposées

Exemple :
Quelle lettre est à l'opposé de la lettre B?
Réponse : la lettre D. Les lettres A et E sont adjacentes sur les deux cubes et E est à la même position, ainsi les deux autres lettres sont forcément opposées.

Règle 3 : Si sur 2 dés une seule face est commune et à la même position, alors les faces opposées ont la même position

Exemple :
Quelle lettre est à l'opposé de la lettre B?
Réponse : la lettre D. La lettre A est commune et à la même position sur les 2 dés, ainsi la lettre B est opposée à la lettre D (et C à E).

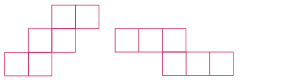
Il existe 11 patrons du cube

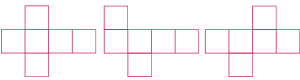
L'analyse du patron permet de trouver rapidement le cube qui en résulte.

Exemple 1 :

Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.

Exemple 2 :

Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.

Exemple 3 :

Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.

Exemple 4 :

Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.

Cas particulier : le dé

L'addition du nombre de points (ou chiffres) des faces opposées d'un dé standard est toujours égale à 7. De plus, la somme de deux faces adjacentes ne peut pas être égale à 7.

Exemple :
Quelle chiffre est à l'opposé du 1?
Réponse : le chiffre 6.
Nous constatons que la somme de deux faces adjacentes n'est jamais égale à 7.

Structure : découpe d'un cube

Si nous découpons ce cube en X parts (ici X = 3), nous obtenons différents types de cubes :

Cubes centraux :
1 seule face visible (représentée par une croix).
Nombre de cubes centraux = 6 (X-2)2 = 6 (3-2)2 = 6

Cubes au milieu :
2 faces visibles (représentées en blanc).
Nombre de cubes au milieu = 12 (X-2) = 12 (3-2) = 12

Cubes au coin :
3 faces visibles (représentées en couleur).
Nombre de cubes au coin = 8 (toujours égal à 8)

Cubes au centre :
0 face visible.
Nombre de cubes au centre = (X-2)3 = 1

Le nombre total de cubes est obtenu par la formule: X3 = 27

Structure : empilement de cubes

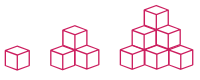
Les figures ci-dessous montrent l'empilement de cubes sur plusieurs étages :

Pour 1 étage, nous avons 1 cube, pour 2 étages 4 cubes, pour 3 étages 10 cubes.

Pour les compter facilement, nous vous conseillons de le faire par colonne en plaçant votre regard de côté. Par exemple, pour la dernière figure, nous obtenons 6 + 3 + 1 = 10.

Un autre exemple d'empilement :

Pour 1 étage, nous avons 1 cube, pour 2 étages 5 cubes, pour 3 étages 14 cubes.

Pour les compter facilement, nous vous conseillons de le faire par ligne en plaçant votre regard de face. Par exemple, pour la dernière figure, nous obtenons 1 + 4 + 9 = 14.

Structure : nombre de faces

Dans certains exercices, vous devrez compter le nombre de faces d'une structure.

Exemple :
Réponses : 12 et 9.

Proposer une amélioration, signaler une erreur ...